Conférences invitées

Nous avons le plaisir d'annoncer quatre présentations invitées : Julien Tierny (Sorbonne Université) va nous parler de son projet Topology ToolKit, Jeanne Pellerin et Estelle Dirand (Total) nous parleront des défis de simulation numérique de panneaux solaires, et Franck Ledoux (CEA) nous exposera le lien entre les problématiques de maillage et l'informatique graphique. Last, but not least, Nicolas Mellado va nous parler de l'analyse des nuages de points.

Julien Tierny : An Introduction to Topological Data Analysis with the Topology ToolKit

Topological Data Analysis (TDA) is a recent area of computer science that focuses on discovering intrinsic structures hidden in data. Based on solid mathematical tools such as Morse theory and Persistent Homology, TDA enables the robust extraction of the main features of a data set into stable, concise, and multi-scale descriptors that facilitate data analysis and visualization.

In this talk, I will give an intuitive overview of the main tools used in TDA (persistence diagrams, Reeb graphs, Morse-Smale complexes, etc) with applications to concrete use cases in computational fluid dynamics, medical imaging, quantum chemistry, and climate modeling. This talk will be illustrated with results produced with the "Topology ToolKit" (TTK), an open-source library (BSD license) that we develop with collaborators to showcase our research. Tutorials for re-producing these experiments are available on the TTK website: https://topology-tool-kit.github.io/

Nicolas Mellado: Introduction to Scale-Space analysis for 3d acquired point clouds

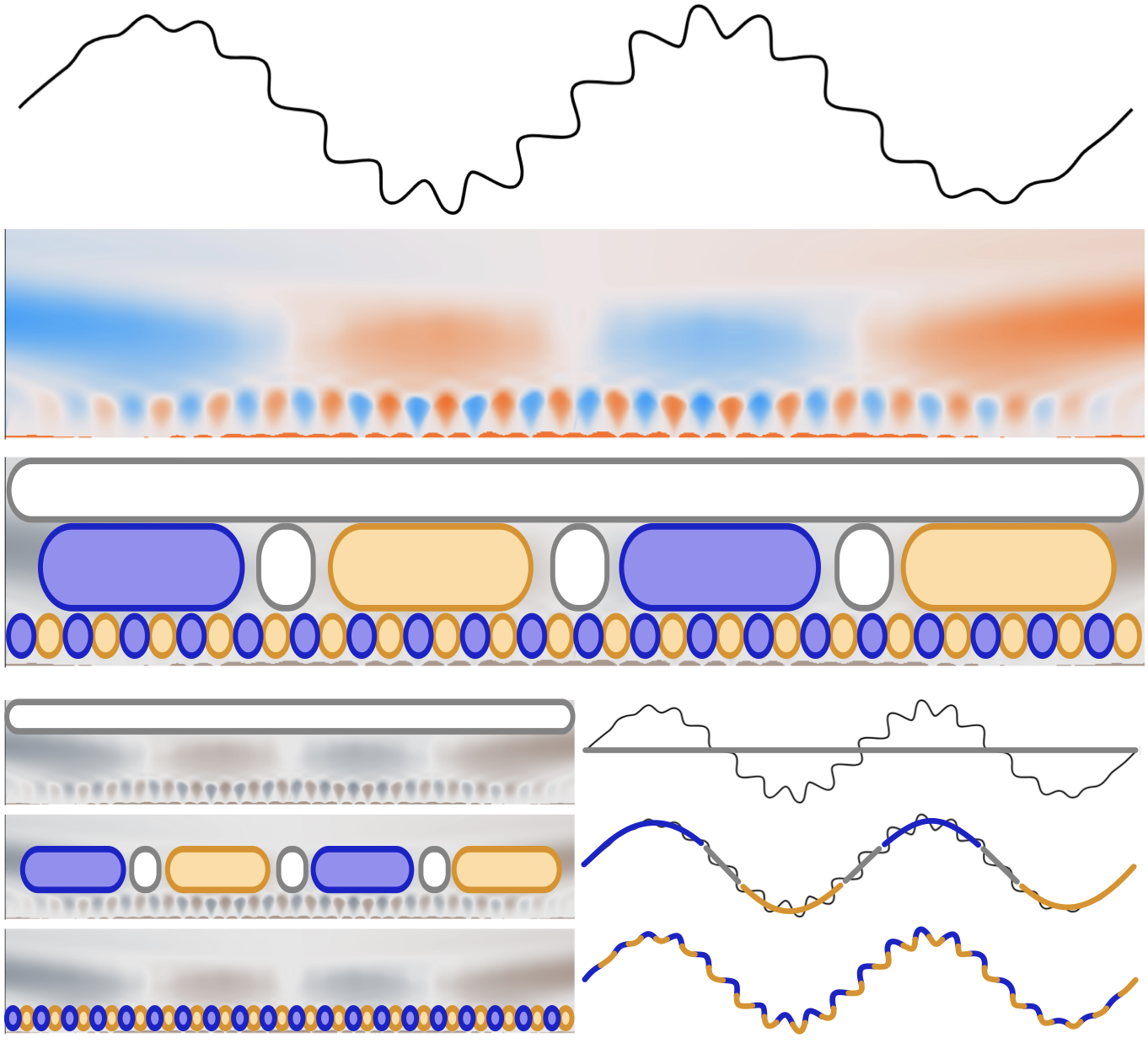
The Scale-Space Theory (SST) is a standard analysis tools for structured signals such as images and curves. The key idea of SST is to track changes of a signal derivatives while applying a smoothing operator. Developed from the eighties, this theory had a strong impact on Computer Graphics, Computer Vision and Image Processing tasks, the most famous example being probably the Scale-Invariant Feature Transform (SIFT).

In this talk, I’ll present how the ideas behind the Scale-Space Theory can be adapted to 3d point clouds analysis in order to detect pertinent scales and structures. I will present the main challenges raised by the study of unstructured point clouds, which do not provide an intrinsic parametrization (in contrat to images) for derivatives computations. I will then introduce the ideas of scale derivatives and stability analysis for pertinent scale extraction. I will then illustrate how these ideas can be applied to relative scale factor estimation between shapes, primitive extraction using persistence analysis, and interactive geometric labeling using deep learning.

Franck Ledoux : Maillage structuré pour le calcul scientifique : Et si la solution venait de l’informatique graphique?

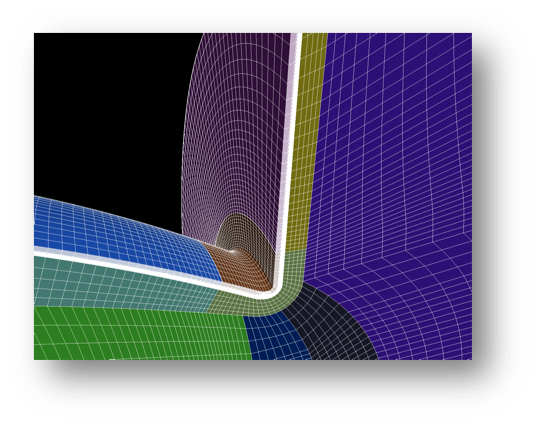
Dans les codes de simulation numérique qui modélisent des phénomènes physiques à l’aide de systèmes d’équations aux dérivées partielles, les maillages sont utilisés pour discrétiser la géométrie d’étude et fournir un support discret aux schémas numériques mis en oeuvre. Selon les domaines étudiés (structure, fluide, interaction laser-plasma,…) et les méthodes numériques utilisées, le maillage doit disposer de caractéristiques spécifiques. Dans cet exposé, nous nous intéressons à une catégorie bien particulière de maillages: les maillages hexaédriques structurés par blocs. Ces maillages indispensables pour de nombreux codes de simulation sont aujourd’hui créés manuellement par des ingénieurs experts à l’aide de logiciels interactifs 3D complexes, ce qui peut prendre plusieurs jours à plusieurs semaines.

Alors que la croissance permanente et régulière des puissances de calculs délivrées par les supercalculateurs permet aux codes de simulation numériques modernes de résoudre des problèmes multi-physiques de plus en plus complexes, le goulot d’étranglement devient l’incapacité à générer de manière rapide les maillages souhaités. Et cela d’autant plus que l’on souhaite considérer des géométries de plus en plus réalistes. Dans ce contexte, la demande est grande pour accélérer le processus de génération de maillages. Alors que la communauté en maillage pour le calcul scientifique échoue à trouver une solution au problème du maillage hexaédrique structuré par blocs, il est intéressant de se demander si des approches issues de l’informatique graphique ne pourraient pas fournir les solutions escomptées.

Après avoir exposé la problématique du maillage en simulation numérique, la présentation sera consacrée à comprendre les caractéristiques des maillages hexaédriques, illustrer comment ces maillages sont créés par des ingénieurs en simulation numérique et voir si différents travaux issus de la communauté de l’informatique graphique ne pourrait pas fournir des solutions.

Jeanne Pellerin et Estelle Dirand : De la géométrie à la visualisation haute-performance : défis en simulation numérique autour des panneaux solaires

La modélisation et la simulation numérique sont des outils fondamentaux en ingénierie, ils permettent notamment d’évaluer et de prédire les propriétés des installations de production d’énergies renouvelables comme les panneaux solaires. Dans cette présentation, nous détaillerons différents challenges rencontrés par Total en modélisation 3D, maillage, simulation numérique, calcul haute performance et visualisation scientifique liés à l’optimisation de la production des panneaux photovoltaïques. Nous nous intéresserons plus particulièrement à l’impact de l’environnement désertique sur l’efficacité des panneaux, et à la prédiction de leur niveau de salissure. Cette simulation de particules implique notamment de calculer de manière intensive l’influence de la taille des particules, du profil du vent et de développer des stratégies d’analyse des données efficaces.